El radar ha avanzado mucho desde finales del siglo XIX y ha evolucionado hasta convertirse en un conjunto de tecnologías que actualmente admite un amplio abanico de aplicaciones.

Estas van desde el sencillo, asequible y compacto radar de onda continua (CW), utilizado por las fuerzas policiales para atrapar a los conductores que superan los límites de velocidad, hasta complejas antenas en fase activa utilizadas en sistemas de radar terrestres, navales y aéreos. Una antena en fase activa o radar de antenas activas orientadas electrónicamente (AESA) típicos se componen de cientos o miles de módulos transmisores/receptores (T/R), y esto es posible gracias a los dispositivos de estado sólido de altas prestaciones.
A medida que las tecnologías de radar llegan a frecuencias más altas y anchos de banda más amplios, han ido apareciendo nuevas aplicaciones imposibles de imaginar anteriormente. La obtención de imágenes por microondas de banda ultraancha no ionizante de bajo coste proporciona información distinta de la que aportan otras técnicas de obtención de imágenes existentes y ofrece aplicaciones prometedoras en el campo médico y de la atención sanitaria. El reconocimiento de gestos por radar con una resolución inferior al milímetro ofrece a los consumidores nuevas formas de interactuar con los dispositivos1. Las tecnologías de radar también han hecho realidad la conducción autónoma y los drones, con capacidades de autonomía y para prevenir colisiones. La banda de THz, con sus singulares propiedades espectrales respecto a contenidos químicos y biológicos, atrae por igual a las comunidades científicas y no científicas con aplicaciones potenciales en obtención de imágenes, sensores y detección. Puesto que los radares ofrecen cada vez más aplicaciones, nos gustaría hacer un breve repaso de los sempiternos principios del radar.

Principio de funcionamiento
La esencia del radar es la capacidad para recopilar información física sobre uno o varios objetivos: ubicación, velocidad, dirección, forma, identidad o su simple presencia. Esto se consigue procesando ondas electromagnéticas reflejadas en el caso de los radares primarios, o a partir de una respuesta transmitida en el caso de los radares secundarios. En la mayoría de las implementaciones, el sistema de radar genera una señal de RF o microondas pulsada y la dirige hacia el objetivo en cuestión. Luego, la misma antena que ha transmitido la señal la vuelve a recibir.
El diagrama de bloques básico de un sistema de radar de impulsos es el que puede verse en la Figura 1. En este diagrama, el temporizador principal o generador de frecuencia de repetición de pulso (PRF) se muestra como el bloque central del sistema. El generador de PRF desempeña un papel importante para sincronizar todos los componentes del sistema de radar a través de conexiones con el modulador de pulsos, el duplexor o el conmutador de transmisión/recepción, y el procesador de pantalla. Además, las conexiones con el receptor proporcionarían filtrado para la protección del front-end o el control de ganancia temporizado, como el control de tiempo de sensibilidad (STC).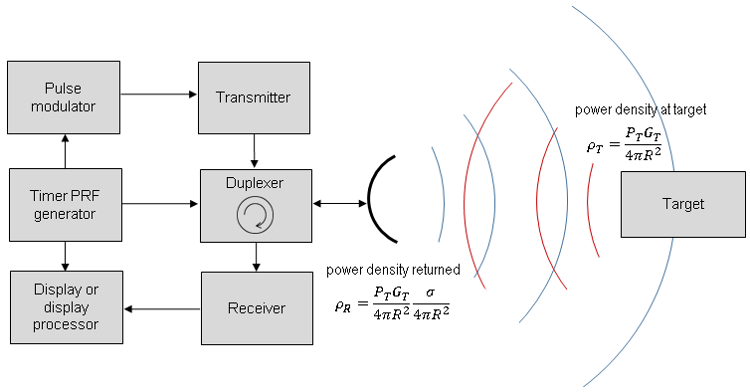

 
Figura 1. Ejemplo de diagrama de bloques para un sistema de radar de pulsos

Explicación de la ecuación de radar
La ecuación de radar describe las variables de rendimiento más importantes de un radar y proporciona los fundamentos para comprender las medidas que se toman con el fin de garantizar un rendimiento óptimo. La ecuación puede presentarse de muchas formas distintas. La Ecuación 1 muestra una forma de ecuación de radar que proporciona el alcance máximo de un radar en metros. Para comprender mejor la ecuación planteada y las hipótesis empleadas, lo mejor es que los lectores repasen la derivación2.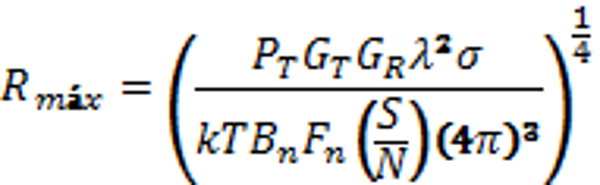


 (1)

Donde:
  R    = distancia máxima en metros
  P_T    = potencia transmitida en vatios
  G_T   = ganancia de la antena de transmisión
  G_R   = ganancia de la antena de recepción
  λ    = longitud de onda de la señal del radar en metros
  α    = sección radar (RCS) del objetivo en metros cuadrados
  k   = constante de Boltzmann
  T   = temperatura ambiente en grados Kelvin
  B_n    = ancho de banda del ruido del receptor en hercios
  F_n    = figura de ruido
  S/N  = mínima relación señal-ruido necesaria

La derivación empieza con el análisis de un modelo de dispersión esférica simple de propagación para un radiador isotrópico (o antena de fuente puntual). Puesto que los sistemas de radar emplean antenas direccionales para concentrar la energía radiada en el objetivo, la ganancia de la antena se define como la relación entre la potencia dirigida hacia el objetivo y la potencia de una antena isotrópica ideal. La ecuación refleja la ganancia directiva de la antena con G_T  y G_R para transmitir y recibir, respectivamente. Si se utiliza la misma antena para transmitir y recibir, la ecuación puede simplificarse sustituyendo los dos términos por G .
Parte de la densidad de la potencia transmitida que llega al objetivo se reflejará en varias direcciones, mientras que parte de la energía volverá a radiarse hacia el sistema de radar. La cantidad de esa densidad de potencia incidente que se vuelve a radiar al radar es una función de la sección radar (RCS o α ) del objetivo. La RCS (α ) se expresa en unidades de área y es una medida del tamaño del objetivo visto por el radar.
La antena del radar interceptará una parte de esa señal reflejada por el objetivo. Esta potencia de señal será igual a la densidad de potencia de retorno en la antena multiplicada por el área efectiva de la antena. Los principales factores que limitan el receptor son el ruido y la relación señal-ruido ( S/N ) resultante.
La potencia de ruido (límite teórico) en la entrada del receptor se describe como el ruido de Johnson o ruido térmico. Es una de las consecuencias del movimiento aleatorio de los electrones, y es proporcional a la temperatura. La potencia de ruido disponible en la salida del receptor será siempre más elevada que el ruido de Johnson. Esto se debe al ruido extra generado dentro del receptor. Por consiguiente, la Ecuación 1 ha tenido en cuenta el ruido generado dentro del receptor al multiplicar la potencia del ruido de Johnson por el factor de ruido F_n y la ganancia del receptor.
La Ecuación 1 describe el alcance máximo del objetivo de nuestro radar a partir de la potencia del transmisor, la ganancia de la antena, la RCS del objetivo, la figura de ruido del sistema y la relación señal-ruido mínima. En realidad, se trata de un modelo simplista del rendimiento del sistema. Existen muchos factores que también afectarán a dicho rendimiento, incluidas las modificaciones de las hipótesis adoptadas para derivar esta ecuación. Otros dos elementos que deberían tenerse en cuenta son las pérdidas del sistema y la integración de pulsos que pueden aplicarse durante el procesamiento de la señal. Las pérdidas del sistema se encontrarán tanto en la ruta de transmisión L_T  como en la de recepción L_R.
En una aplicación clásica de radar de pulsos, podríamos asumir que se recibirían varios pulsos desde un objetivo determinado para cada posición de la antena del radar (como la anchura del haz de la antena del radar es mayor que cero, podemos asumir que el radar permanecerá en cada objetivo durante un periodo de tiempo) y, por tanto, podrían integrarse para mejorar el rendimiento del sistema de radar. Puesto que esta integración quizá no sea ideal, se utilizará un término de eficiencia de integración E_i(n) basado en el número de pulsos integrados para describir la mejora en la integración. Al incluir estos términos, la ecuación radar queda así: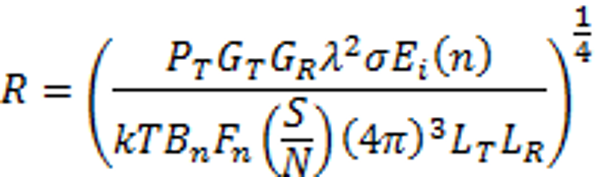
   (2)

Donde:
  E_i(n)  = factor de eficiencia de integración
  L_T    = pérdidas en la ruta de transmisión
  LR    = pérdidas en la ruta de recepción

Para radares de varias antenas, el alcance del radar aumentará proporcionalmente al número de elementos, siempre que todos los elementos ofrezcan un rendimiento idéntico.

Conclusiones sobre la ecuación radar
La potencia de la señal en el receptor de radar es directamente proporcional a la potencia transmitida, la ganancia de la antena (o tamaño de apertura) y la sección radar (RCS); es decir, el grado hasta el cual un objetivo refleja la señal de radar. Y lo que quizá resulta más importante, es inversamente proporcional a la cuarta potencia de la distancia al objetivo. A la vista de la gran atenuación que se produce mientras la señal viaja hacia el objetivo y desde este, es muy conveniente tener una potencia elevada. Sin embargo, resulta complicado disponer de una potencia elevada a causa de problemas prácticos como el calor, el colapso de tensión, los requisitos de potencia dinámica, el tamaño del sistema y el coste.

En el próximo artículo, abordaremos las características, las técnicas de compresión y la medida de la señal pulsada del radar.
Referencias:
1.    https://atap.google.com/soli/
2.    http://literature.cdn.keysight.com/litweb/pdf/5992-1386EN.pdf?id=2715324

Autor:

Giovanni D’Amore
Marketing Brand Manager - EMEAI
RF & Microwave Products
Keysight Technologies

El radar ha avanzado mucho desde finales del siglo XIX y ha evolucionado hasta convertirse en un conjunto de tecnologías que actualmente admite un amplio abanico de aplicaciones. Estas van desde el sencillo, asequible y compacto radar de onda continua (CW), utilizado por las fuerzas policiales para atrapar a los conductores que superan los límites de velocidad, hasta complejas antenas en fase activa utilizadas en sistemas de radar terrestres, navales y aéreos. Una antena en fase activa o radar de antenas activas orientadas electrónicamente (AESA) típicos se componen de cientos o miles de módulos transmisores/receptores (T/R), y esto es posible gracias a los dispositivos de estado sólido de altas prestaciones.

A medida que las tecnologías de radar llegan a frecuencias más altas y anchos de banda más amplios, han ido apareciendo nuevas aplicaciones imposibles de imaginar anteriormente. La obtención de imágenes por microondas de banda ultraancha no ionizante de bajo coste proporciona información distinta de la que aportan otras técnicas de obtención de imágenes existentes y ofrece aplicaciones prometedoras en el campo médico y de la atención sanitaria. El reconocimiento de gestos por radar con una resolución inferior al milímetro ofrece a los consumidores nuevas formas de interactuar con los dispositivos¹. Las tecnologías de radar también han hecho realidad la conducción autónoma y los drones, con capacidades de autonomía y para prevenir colisiones. La banda de THz, con sus singulares propiedades espectrales respecto a contenidos químicos y biológicos, atrae por igual a las comunidades científicas y no científicas con aplicaciones potenciales en obtención de imágenes, sensores y detección. Puesto que los radares ofrecen cada vez más aplicaciones, nos gustaría hacer un breve repaso de los sempiternos principios del radar.

Principio de funcionamiento

La esencia del radar es la capacidad para recopilar información física sobre uno o varios objetivos: ubicación, velocidad, dirección, forma, identidad o su simple presencia. Esto se consigue procesando ondas electromagnéticas reflejadas en el caso de los radares primarios, o a partir de una respuesta transmitida en el caso de los radares secundarios. En la mayoría de las implementaciones, el sistema de radar genera una señal de RF o microondas pulsada y la dirige hacia el objetivo en cuestión. Luego, la misma antena que ha transmitido la señal la vuelve a recibir.

El diagrama de bloques básico de un sistema de radar de impulsos es el que puede verse en la Figura 1. En este diagrama, el temporizador principal o generador de frecuencia de repetición de pulso (PRF) se muestra como el bloque central del sistema. El generador de PRF desempeña un papel importante para sincronizar todos los componentes del sistema de radar a través de conexiones con el modulador de pulsos, el duplexor o el conmutador de transmisión/recepción, y el procesador de pantalla. Además, las conexiones con el receptor proporcionarían filtrado para la protección del front-end o el control de ganancia temporizado, como el control de tiempo de sensibilidad (STC).

Figura 1. Ejemplo de diagrama de bloques para un sistema de radar de pulsos

Explicación de la ecuación de radar

La ecuación de radar describe las variables de rendimiento más importantes de un radar y proporciona los fundamentos para comprender las medidas que se toman con el fin de garantizar un rendimiento óptimo. La ecuación puede presentarse de muchas formas distintas. La Ecuación 1 muestra una forma de ecuación de radar que proporciona el alcance máximo de un radar en metros. Para comprender mejor la ecuación planteada y las hipótesis empleadas, lo mejor es que los lectores repasen la derivación².

                                              (1)

Donde:

         = distancia máxima en metros

         = potencia transmitida en vatios

         = ganancia de la antena de transmisión

         = ganancia de la antena de recepción

          = longitud de onda de la señal del radar en metros

          = sección radar (RCS) del objetivo en metros cuadrados

           = constante de Boltzmann

           = temperatura ambiente en grados Kelvin

        = ancho de banda del ruido del receptor en hercios

         = figura de ruido

          = mínima relación señal-ruido necesaria

La derivación empieza con el análisis de un modelo de dispersión esférica simple de propagación para un radiador isotrópico (o antena de fuente puntual). Puesto que los sistemas de radar emplean antenas direccionales para concentrar la energía radiada en el objetivo, la ganancia de la antena se define como la relación entre la potencia dirigida hacia el objetivo y la potencia de una antena isotrópica ideal. La ecuación refleja la ganancia directiva de la antena con y para transmitir y recibir, respectivamente. Si se utiliza la misma antena para transmitir y recibir, la ecuación puede simplificarse sustituyendo los dos términos por .

Parte de la densidad de la potencia transmitida que llega al objetivo se reflejará en varias direcciones, mientras que parte de la energía volverá a radiarse hacia el sistema de radar. La cantidad de esa densidad de potencia incidente que se vuelve a radiar al radar es una función de la sección radar (RCS o ) del objetivo. La RCS () se expresa en unidades de área y es una medida del tamaño del objetivo visto por el radar.

La antena del radar interceptará una parte de esa señal reflejada por el objetivo. Esta potencia de señal será igual a la densidad de potencia de retorno en la antena multiplicada por el área efectiva de la antena. Los principales factores que limitan el receptor son el ruido y la relación señal-ruido () resultante.

La potencia de ruido (límite teórico) en la entrada del receptor se describe como el ruido de Johnson o ruido térmico. Es una de las consecuencias del movimiento aleatorio de los electrones, y es proporcional a la temperatura. La potencia de ruido disponible en la salida del receptor será siempre más elevada que el ruido de Johnson. Esto se debe al ruido extra generado dentro del receptor. Por consiguiente, la Ecuación 1 ha tenido en cuenta el ruido generado dentro del receptor al multiplicar la potencia del ruido de Johnson por el factor de ruido y la ganancia del receptor.

La Ecuación 1 describe el alcance máximo del objetivo de nuestro radar a partir de la potencia del transmisor, la ganancia de la antena, la RCS del objetivo, la figura de ruido del sistema y la relación señal-ruido mínima. En realidad, se trata de un modelo simplista del rendimiento del sistema. Existen muchos factores que también afectarán a dicho rendimiento, incluidas las modificaciones de las hipótesis adoptadas para derivar esta ecuación. Otros dos elementos que deberían tenerse en cuenta son las pérdidas del sistema y la integración de pulsos que pueden aplicarse durante el procesamiento de la señal. Las pérdidas del sistema se encontrarán tanto en la ruta de transmisión como en la de recepción .

En una aplicación clásica de radar de pulsos, podríamos asumir que se recibirían varios pulsos desde un objetivo determinado para cada posición de la antena del radar (como la anchura del haz de la antena del radar es mayor que cero, podemos asumir que el radar permanecerá en cada objetivo durante un periodo de tiempo) y, por tanto, podrían integrarse para mejorar el rendimiento del sistema de radar. Puesto que esta integración quizá no sea ideal, se utilizará un término de eficiencia de integración basado en el número de pulsos integrados para describir la mejora en la integración. Al incluir estos términos, la ecuación radar queda así:

                                          (2)

Donde:

   = factor de eficiencia de integración

         = pérdidas en la ruta de transmisión

         = pérdidas en la ruta de recepción

Para radares de varias antenas, el alcance del radar aumentará proporcionalmente al número de elementos, siempre que todos los elementos ofrezcan un rendimiento idéntico.

Conclusiones sobre la ecuación radar

La potencia de la señal en el receptor de radar es directamente proporcional a la potencia transmitida, la ganancia de la antena (o tamaño de apertura) y la sección radar (RCS); es decir, el grado hasta el cual un objetivo refleja la señal de radar. Y lo que quizá resulta más importante, es inversamente proporcional a la cuarta potencia de la distancia al objetivo. A la vista de la gran atenuación que se produce mientras la señal viaja hacia el objetivo y desde este, es muy conveniente tener una potencia elevada. Sin embargo, resulta complicado disponer de una potencia elevada a causa de problemas prácticos como el calor, el colapso de tensión, los requisitos de potencia dinámica, el tamaño del sistema y el coste.

En el próximo artículo, abordaremos las características, las técnicas de compresión y la medida de la señal pulsada del radar.

Referencias:

1.       https://atap.google.com/soli/

2.       http://literature.cdn.keysight.com/litweb/pdf/5992-1386EN.pdf?id=2715324